Rigid body game physics 3

25 Nov 2019

part 1 part 2 part 3 part 4 part 5 part 6

The following article is based on Hubert Eichner’s article on inequality constraints.

Inequality Constraints for Resting Contacts

Contact points (resting contacts) are represented as inequality constraints. In contrast to a joint, a resting contact can only create repellent forces and no attracting forces. Similar to a joint constraint, the resting contact is represented using a function C(y(t)). Here C is one-dimensional and it is basically the distance of the two objects at the contact point. The inequality constraint of the resting contact is with the matrix J having one row and twelve columns. Instead of anchor points, one uses vectors ri and rj from the center of each object to the contact point. Using the contact normal n the inequality constraint becomes: The rotational component can be simplified as shown below: 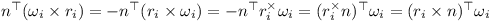Thus the linear components of J are And the angular components of J are The correction term depends on the distance d. I.e. if the distance is negative, a correction is required so that the objects do not penetrate each other any more.

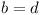
Sequential Impulses (updated)

The impulses generated by contact constraints and joint constraints are accumulated in a loop. The (cumulative) λ obtained for contact constraint furthermore is clipped to be greater or equal to zero. Note that it has to be the cumulative value which is clipped. The algorithm for solving the joint and contact constraints becomes:

• for each iteration
  • for each joint
    1. compute Jacobian J and correction vector b
    2. predict speed u
    3. compute λ
    4. compute the impulse P
    5. add P to accumulated impulses of the two objects
  • for each resting contact
    1. subtract old impulses P from previous iteration from accumulated impulses of the two objects
    2. compute Jacobian J and correction vector b
    3. predict speed u
    4. compute new λ and clip it to be greater or equal to zero
    5. compute the impulse P
    6. add P to accumulated impulses of the two objects
• use impulses and external forces to perform Runge Kutta integration step

The sequential impulse iterations have to be performed four times when using the Runge-Kutta method. The value λ is stored as Pn for limiting friction impulses lateron.